dB/voltage, What is the relationship?
In a world of diverse equipment is there some sense we can make of the whole thing? Well lets see.
Now the first spec were going to discuss is 0dBm =0.775 volts= 1 milliwatt but only @ exactly 600 ohms...this is then a spec relative to telephone lines.
So when we specify 0dBu = 0.775 v= 1mw we are specifying 'unloaded' in terms of current audio equipment where great distances are not the issue as in telephone circuits. This is a convenient measure for preamp design but it's not so convenient in terms of explanations...
0dBV is simpler to explain and therefore, 0dBV (note upper case V) = 1 volt
Most audio equipment is specified as working at either 'Plus 4' or 'Minus 10', but what does that mean in practice? 'Plus 4' means +4dBu, an operating level adopted in pro audio due to historic rather than purely logical reasons, and corresponding to an RMS signal level of 1.23 Volts. This is a fairly convenient figure for use with modern op-amp circuitry as it leaves a sensible amount of headroom before the circuitry runs into clipping.
Therefore:
+4 = +4dBu = 1.23volts RMS
The so-called 'Minus 10' level was introduced along with semi-pro recording gear and is largely a Japanese concept. Correctly stated, this is -10dBV which corresponds to 0.316 Volts -- roughly a third of a volt. Again this is reasonable for use with op-amp circuitry, but many purists feel the +4dBu system provides a better balance between noise and headroom.
Therefore:
-10 = -10dBv = 0.316volts RMS
There is a standard of consumer gear that we as pro audio types run into with some keyboards (mainly) that were developed that way to interface with consumer level gear. This standard is :
-20 = -20dBv = .1 volts RMS
This can cause noise problems in P.A. systems where so much makeup gain is needed that the signal to noise is greater than the gain structure available...
The formula's for those of you math types...
When comparing two power levels, the number of dBs difference may be calculated by the equation:
Number of dBs = 10 log (P1/P2) where P1 and P2 are the two powers being compared and where the log is to the base 10.
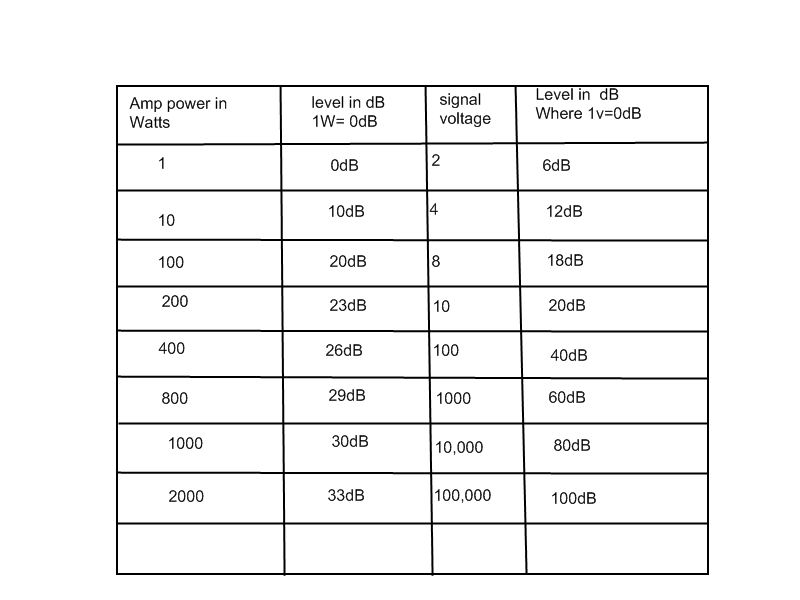
If you don't understand how logs work, don't worry because nobody actually works out dB levels in this way -- well hardly anyone. However, there are some useful figures that you should remember, the most common being that 3dB represents a doubling in power. It follows then that a 10 Watt amplifier can produce 3dB more power than a 5 Watt amplifier. Similarly, a 20 Watt amplifier can produce 3dB more power than a 10 Watt amplifier. So, how much more powerful is a 20 Watt amplifier than a 5 Watt amplifier? Simple, just add two lots of 3dB, which gives you 6dB.
Because of the mathematical relationship between power and voltage, the calculations are slightly different when it comes to working out voltage ratios in dBs. Here the equation is:
Number of dBs = 20 log (P1/P2) where P1 and P2 are the two powers being compared and where the log is to the base 10.
Note that we now have a 20 in the equation instead of a 10 which means the answer is twice what it would be for a ratio of powers. In other words, double the voltage and the level goes up by 6dB; halve the voltage and the level goes down by 6dB.
Here is a table to summarize:
Gadget
Now the first spec were going to discuss is 0dBm =0.775 volts= 1 milliwatt but only @ exactly 600 ohms...this is then a spec relative to telephone lines.
So when we specify 0dBu = 0.775 v= 1mw we are specifying 'unloaded' in terms of current audio equipment where great distances are not the issue as in telephone circuits. This is a convenient measure for preamp design but it's not so convenient in terms of explanations...
0dBV is simpler to explain and therefore, 0dBV (note upper case V) = 1 volt
Most audio equipment is specified as working at either 'Plus 4' or 'Minus 10', but what does that mean in practice? 'Plus 4' means +4dBu, an operating level adopted in pro audio due to historic rather than purely logical reasons, and corresponding to an RMS signal level of 1.23 Volts. This is a fairly convenient figure for use with modern op-amp circuitry as it leaves a sensible amount of headroom before the circuitry runs into clipping.
Therefore:
+4 = +4dBu = 1.23volts RMS
The so-called 'Minus 10' level was introduced along with semi-pro recording gear and is largely a Japanese concept. Correctly stated, this is -10dBV which corresponds to 0.316 Volts -- roughly a third of a volt. Again this is reasonable for use with op-amp circuitry, but many purists feel the +4dBu system provides a better balance between noise and headroom.
Therefore:
-10 = -10dBv = 0.316volts RMS
There is a standard of consumer gear that we as pro audio types run into with some keyboards (mainly) that were developed that way to interface with consumer level gear. This standard is :
-20 = -20dBv = .1 volts RMS
This can cause noise problems in P.A. systems where so much makeup gain is needed that the signal to noise is greater than the gain structure available...
The formula's for those of you math types...
When comparing two power levels, the number of dBs difference may be calculated by the equation:
Number of dBs = 10 log (P1/P2) where P1 and P2 are the two powers being compared and where the log is to the base 10.
If you don't understand how logs work, don't worry because nobody actually works out dB levels in this way -- well hardly anyone. However, there are some useful figures that you should remember, the most common being that 3dB represents a doubling in power. It follows then that a 10 Watt amplifier can produce 3dB more power than a 5 Watt amplifier. Similarly, a 20 Watt amplifier can produce 3dB more power than a 10 Watt amplifier. So, how much more powerful is a 20 Watt amplifier than a 5 Watt amplifier? Simple, just add two lots of 3dB, which gives you 6dB.
Because of the mathematical relationship between power and voltage, the calculations are slightly different when it comes to working out voltage ratios in dBs. Here the equation is:
Number of dBs = 20 log (P1/P2) where P1 and P2 are the two powers being compared and where the log is to the base 10.
Note that we now have a 20 in the equation instead of a 10 which means the answer is twice what it would be for a ratio of powers. In other words, double the voltage and the level goes up by 6dB; halve the voltage and the level goes down by 6dB.
Here is a table to summarize:

Gadget
0